|
In the previous installment, we presented a concrete example of pricing a European option. In this follow-up post we are going to provide an example of valuing American options. The key difference between American and European options relates to when the options can be exercised:
An exact analytical solution exists for European options. For American options, however, we have to use numerical methods such as Binomial Tree (i.e. Lattice) or approximations. The post entitled How to Price a Convertible Bond provides an example of the Binomial Tree approach. The Binomial Tree model is an accurate one. However, its main drawback is that it’s slow. Consequently, several researchers have developed approximate solutions that are faster. In this example we’re going to use the Barone-Andesi-Whaley approximation [1]. The Barone-Adesi and Whaley Model has the advantages of being fast, accurate and inexpensive to use. It is most accurate for options that will expire in less than one year. The Black-Scholes Model is appropriate for European options, that is, options that may be exercised only on the expiration date. The Barone-Adesi and Whaley Model is designed for American options, which are options that may be exercised at any time before they expire. The Barone-Adesi and Whaley Model takes the value computed by the Black-Scholes Model and adds the value of the early exercise option that is available on American option.. Read more [caption id="attachment_518" align="aligncenter" width="621"] Recall that the important inputs are: Volatility In this example we are going to use historical volatility. We retrieve the historical stock data from Yahoo finance. We then proceed to calculate the daily returns and use them to determine the annual volatility. The resulting volatility is 43%. Detailed calculation is provided in the accompanying Excel workbook. Stock price The stock price is also obtained from Yahoo finance. It is 13.5 as of the valuation date (Aug 22 2018). Dividend The dividend yield is obtained from Yahoo finance. It is 1.2%. Note that for illustration purposes we use continuous instead of discrete dividend. Interest rate The risk-free interest rate is retrieved from Bank of Canada website. Since the tenor of the option is 3 years, we’re going to use the 3-year benchmark yield. It is 2.13% as at the valuation date. We use the Excel calculator again and obtain a price of $3.32 for the American put option. [caption id="attachment_519" align="aligncenter" width="336"] Click on the link below to download the Excel Workbook.
References Barone-Adesi, G. and Whaley, R.E. (1987) Efficient Analytic Approximation of American Option Values The Journal of Finance, 42, 301-320. Originally Published Here: Valuing an American Option-Derivative Pricing in Excel
0 Comments
An option is a financial contract that gives you a right, but not an obligation to buy or sell an underlying at a future time and at a pre-determined price. Specifically, ... an option is a contract which gives the buyer (the owner or holder of the option) the right, but not the obligation, to buy or sell an underlying asset or instrument at a specified strike price on a specified date, depending on the form of the option. The strike price may be set by reference to the spot price (market price) of the underlying security or commodity on the day an option is taken out, or it may be fixed at a discount or at a premium. The seller has the corresponding obligation to fulfill the transaction – to sell or buy – if the buyer (owner) "exercises" the option. An option that conveys to the owner the right to buy at a specific price is referred to as a call; an option that conveys the right of the owner to sell at a specific price is referred to as a put. Read more Excellent textbooks and papers have been written on options pricing theory; see for example Reference [1]. In this post we are going to deal with practical aspects of pricing a European option. We do so through a concrete example. We’re going to price a put option on Barrick Gold, a Canadian mining company publicly traded on the Toronto Stock Exchange under the symbol ABX.TO. For this exercise, we assume that the option is of European style with a strike price of $13. (American style option will be dealt with in the next installment). The option expires in 3 years, and the valuation date is August 22, 2018. [caption id="attachment_484" align="aligncenter" width="540"] The important input parameters are: Volatility In this example we are going to use historical volatility. We retrieve the historical stock data from Yahoo finance. We then proceed to calculate the daily returns and use them to determine the annual volatility. The resulting volatility is 43%. Detailed calculation is provided in the accompanying Excel workbook. Stock price The stock price is also obtained from Yahoo finance. It is 13.5 as at the valuation date. Dividend The dividend yield is obtained from Yahoo finance. It is 1.2%. Note that for illustration purposes we use continuous instead of discrete dividend. Interest rate The risk-free interest rate is retrieved from Bank of Canada website. Since the tenor of the option is 3 years, we’re going to use the 3-year benchmark yield. It is 2.13% as at the valuation date. After obtaining all the required input data, we use QuantlibXL to calculate the price of the option. The calculator returns a price of $3.21. The picture below presents a summary of the valuation inputs and results. [caption id="attachment_482" align="aligncenter" width="306"] In the next installment, we’re going to present an example for American option. Follow the link below to download the Excel Workbook.
References [1] Hull, John C. (2005), Options, Futures and Other Derivatives (6th Ed.), Prentice-Hall
Originally Published Here: VALUING A EUROPEAN OPTION |
Archives
April 2023
|

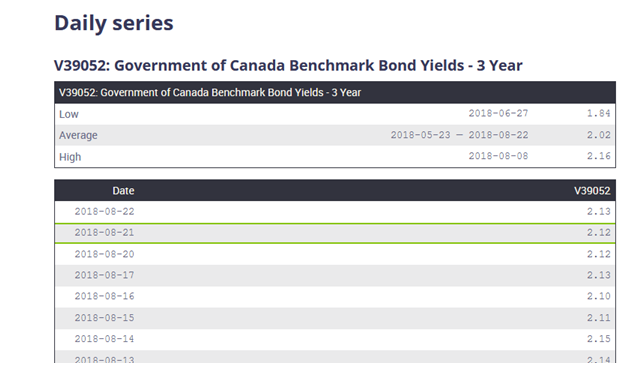 Government of Canada Benchmark Bond Yield. Source: Bank of Canada[/caption]
Government of Canada Benchmark Bond Yield. Source: Bank of Canada[/caption]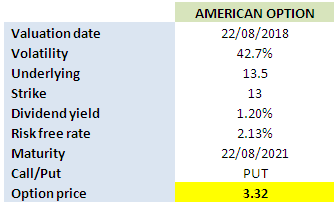 American option valuation in Excel[/caption]
American option valuation in Excel[/caption]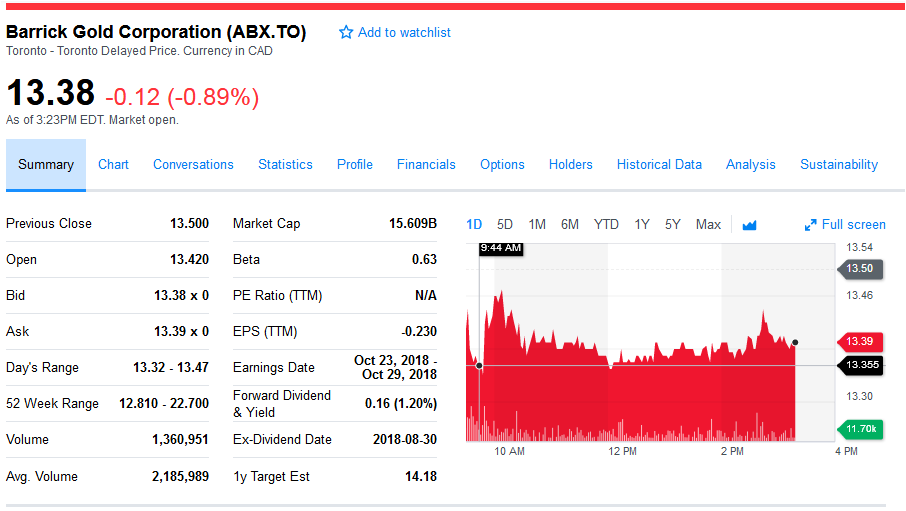 Barrick Gold mining financial data as at Aug 23 2018[/caption]
Barrick Gold mining financial data as at Aug 23 2018[/caption]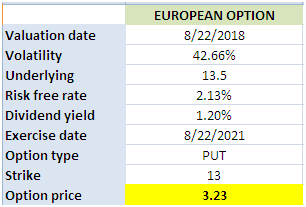 European option valuation in Excel[/caption]
European option valuation in Excel[/caption] RSS Feed
RSS Feed
