|
A lot of research has been devoted to answering the question: do options price in the volatility risks correctly? The most noteworthy phenomenon (or bias) is called the volatility risk premium, i.e. options implied volatilities tend to overestimate future realized volatilities. Much less attention is paid, however, to the underlying asset dynamics, i.e. to answering the question: do options price in the asset dynamics correctly? Note that within the usual BSM framework, the underlying asset is assumed to follow a GBM process. So to answer the above question, it’d be useful to use a different process to model the asset price. We found an interesting article on this subject [1]. Instead of using GBM, the authors used a process where the asset returns are auto-correlated and then developed a closed-form formula to price the options. Specifically, they assumed that the underlying asset follows an MA(1) process,
where β represents the impact of past shocks and h is a small constant. We note that After applying some standard pricing techniques, a closed-form option pricing formula is derived which is similar to BSM except that the variance (and volatility) contains the autocorrelation coefficient,
From the above equation, it can be seen that
References [1] Liao, S.L. and Chen, C.C. (2006), Journal of Futures Markets, 26, 85-102. Original Post Here: Is Asset Dynamics Priced In Correctly by Black-Scholes-Merton Model?
0 Comments
Leave a Reply. |
Archives
April 2023
|

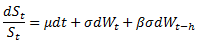
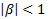 and in case β=0 the price dynamics becomes GBM.
and in case β=0 the price dynamics becomes GBM. RSS Feed
RSS Feed
